|
|
| Summary: |
Basic Production Theory and Production Function: the output from the combinations of inputs. |
| Detail: |
Production refers to the process of converting inputs to outputs.
Inputs are called Factor of Production. It includes:
- Fixed capital: such as machinery, factories, equipment, new technology, factories, buildings, computers, and software.
They usually do not change due to the production of the good, but they are used to produce products or services.
- Working capital: such as raw materials, nuts, lubrication oil, electrical power consumption, and transportation services.
They are the stocks (also called inventories) of finished and semi-finished goods that are consumed in the production process
or made into finished consumer goods in the manufacturing cases. The amount or nature of this type of capital is usually
changed during the production process.
- Labor services: they include labors performing the production activities and entrepreneurs providing management and visions.
- Nature resources: such as land, minerals, and forests.
The short run production function defines the quantity of output relative to the amount of a variable input (factor of production) employed
while holding other fixed inputs constant.
Given the set of all technically feasible combinations of output and inputs, we want to determine a
production process which generates maximum output for a specified set of inputs. Alternatively,
we want to determine the specification of the minimum input requirements needed to produce designated
quantities of output, given available technology.
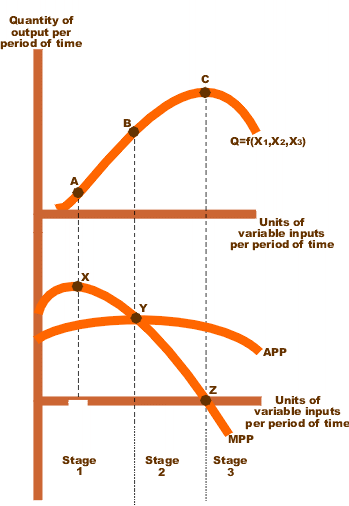
See the following figure for a sample of quadratic production function which depicts the output relative to a variable input.
- Average Physical Product (APP): the total production divided by the number of units of variable input employed.
- Marginal Physical Product (MPP): the change in total output due to a one unit change in the variable input
(in the discrete case) or the rate of change in total output due to an infinitesimally small change in the variable input (in the continuous case).
Diminishing returns:
- Diminishing Marginal returns (Point A): the MPP curve starts to slope down and travels all the way down to the x-axis and beyond.
- Diminishing Average returns (Point B): the intersection of APP curve with MPP curve where the average return will go down.
- Diminishing Total returns (Point C): the total product reduces with every additional unit of input.
Production function stages:
- Stage 1: MPP keeps increasing until it reaches its maximum (see Pint A). Up until this point every additional unit adds more value to the total product than the previous one. From this point onwards, every additional unit adds less to the total product compared to the previous one � MPP starts decreasing. But the average product (APP) is still increasing till MPP touches APP (See Point B). At this point, an additional unit is adding the same value as the average product.
- Stage 2: After Point B, APP starts to reduce because every additional unit is adding less to APP than the average product. MPP decreases when the variable input is increased per unit. However, the average product of fixed inputs (not shown) is still rising, because output is rising while fixed input usage is constant. And the variable input is still being used with increasing output per unit.
- Stage 3: At a point (see Point C), variable inputs are over-utilized, their presence on the margin obstructs the production process rather than enhancing it. Both MPP and APP declines when the variable input is increased.
The optimimum point is between stage 2 and 3 where you can reach the highest possible output from a fixed input.
Production functions:
Q = f(X1,X2,X3,...,Xn)
where
Q=quantity of output;
X1,X2,X3,...,Xn=quantities of factor inputs such as capital, labor,land or raw material.
Q can be a scalar value or a vector Rk.
- Linear function: Q = a + bX1 + cX2 + dX3 + ...
- Cobb-Douglas: Q=aXb1Xc2 (constant elasticity of substitution: generalized form of the Cobb-Douglas function with quadratic production function)
- Leontief production function: Q=min(aX1,bX2,...)
See more details in Production Function.
|
| Figures: |
|
| URL: |
http://en.wikipedia.org/wiki/Production_theory_basics
|
| Subject: |
Cost and Profit |
|
|
|